An annuity is a financial contract that involves making periodic payments to an investor or lender until the end of the agreement. Calculating the present value (PV) of future annuity payments helps an investor understand the amount of money that an annuity represents in today’s dollars.
Let’s go through the different present value of annuity types and the PV of annuity formulas to help you make calculations as well as informed investment decisions.
What Is the Present Value of an Annuity?
The present value of an annuity is the application of the time value of money. It’s the cash amount that a future stream of payments would be worth today when discounted to the present at a given interest rate. (Check out this present value of annuity table.)
The time value of money states that money received today is worth more than the same amount of money you’d receive in the future. For example, getting $10,000 now is preferable to receiving $10,000 in 5 years. That’s because money has the potential to increase in value over a period of time, like deposits in a bank savings account earning interest and increasing in value.
Using Present Value of Annuity in Business Decisions
There are several situations when you’ll need to use a present value of annuity formula to help inform business-related decisions. Some of these instances include:
- Receiving settlement payments
- Selling patents and/or other rights to a developed product, service or idea
- Investing in another business
For example, knowing how to use the PV of annuity formula can help you decide whether it’s better to take a lump sum of money now or receive annuity payments over a period of time.

Present Value of an Annuity Formulas
Two types of annuity payments are ordinary annuities and annuities due.
- Ordinary Annuity: Payments are received at the end of each time period, which could be weekly, monthly, semi-annually or annually.
- Annuity Due: Payments are made at the beginning of each designated time period.
Here’s how to find the present value of an ordinary annuity and how to calculate the present value of an annuity due.
- PMT = the amount of each payment
- r = the interest rate
- n = the number of periods that payments are made
Present Value of Ordinary Annuity Formula
Present Value of an Annuity Due Formula
So, what’s the difference between present value of ordinary annuity and present value of annuity due formulas? Let’s look at each PV of annuity formula in the following scenario:
You have the opportunity to receive a lump-sum payment of $325,000, or 25 annual payments of $25,000 each. You decide to use a discount rate of 6% to calculate the present value of each type of annuity.
Present value of ordinary annuity:
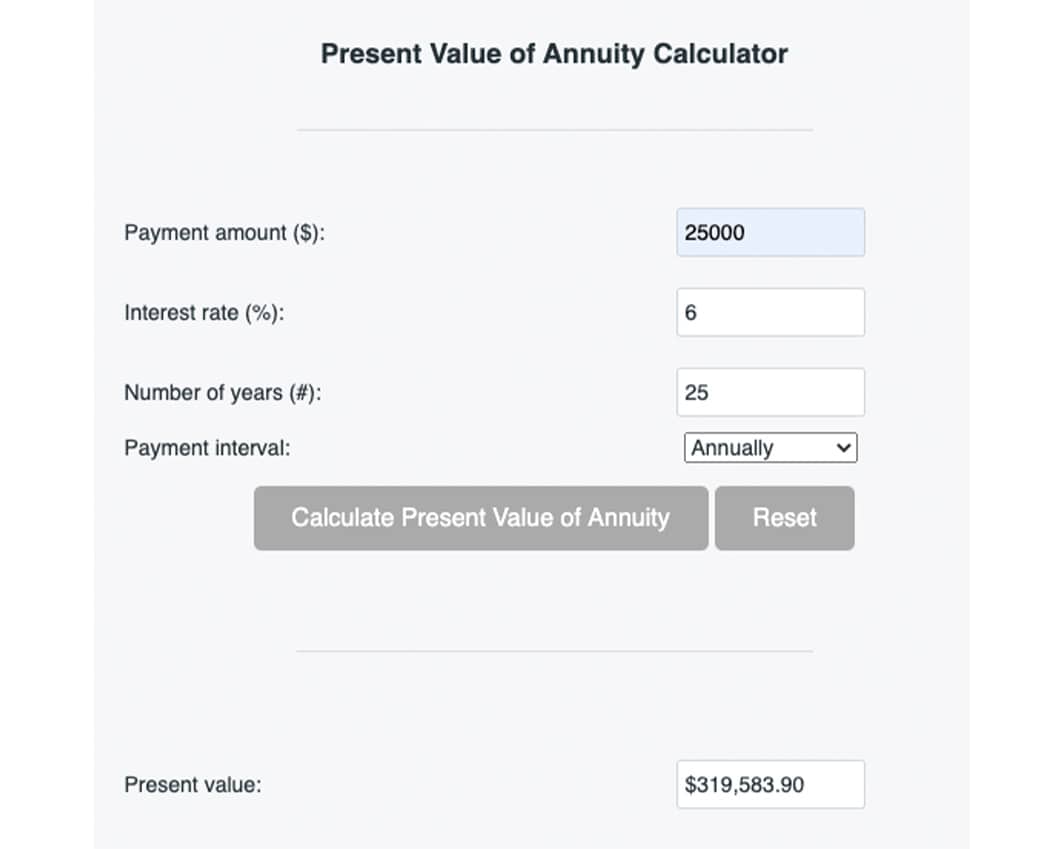
In the case of an ordinary annuity, you’d take the lump-sum payment of $325,000 because it’s higher than the present value.
Present value of an annuity due:

The present value for an annuity due is $338,758.94 is higher than the lump-sum amount. It would make sense to choose the annuity due contract.
Present Value of Annuity Calculator
If your math skills are strong, you can plug the relevant numbers into either formula and work out the PV of annuity on paper or with your regular calculator. However, the web also has several sources if you’re specifically looking for a present value of annuity calculator.
You can find calculators at Financial Mentor and CalculatorSoup.
Present Value of Annuity Example
Suppose Fred, the owner of ABC Corp., developed a new device that helps plumbers solder copper pipe faster, saving a lot of labor hours and reducing the cost of installation. Fred has received a patent but doesn’t have the desire or money it would take to make and market the product himself.
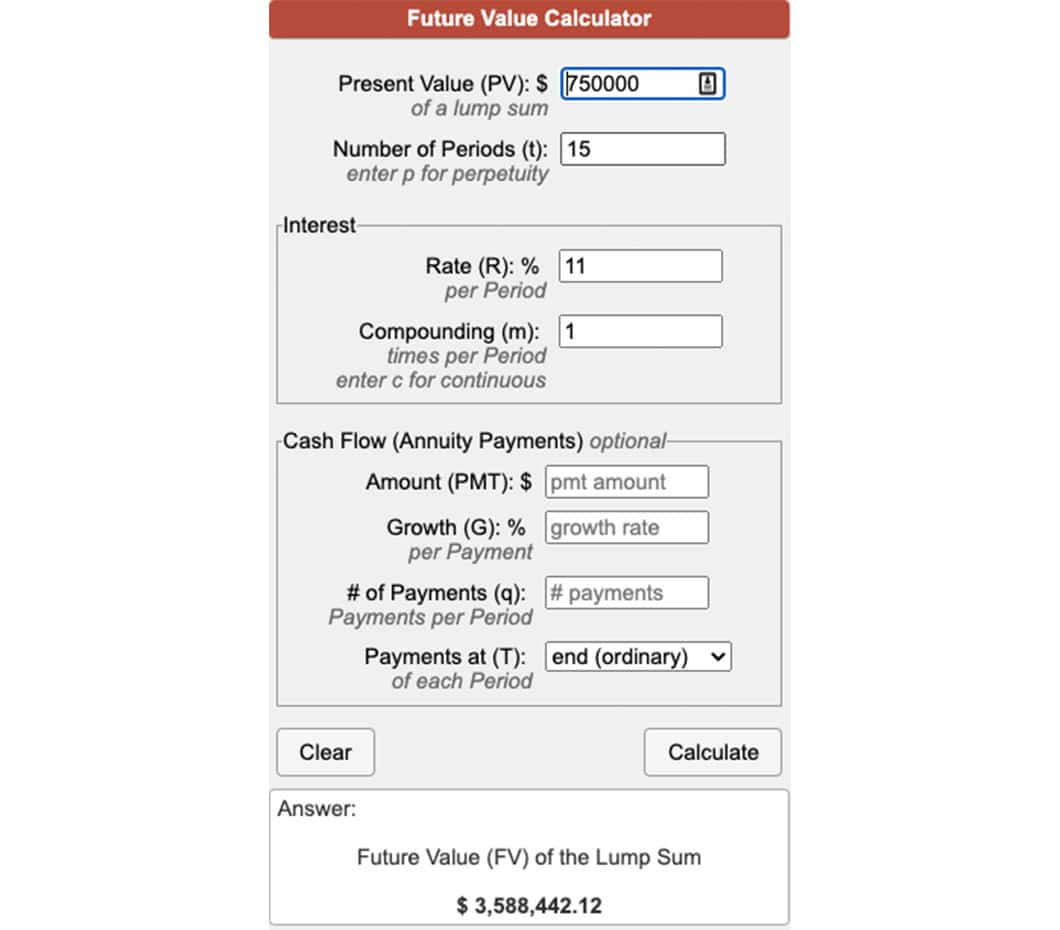
A large plumbing supply company, Giant Tools, has made Fred an offer. Giant proposes an up-front sum of $750,000 to purchase the patent and all rights or the company will pay him $100,000 a year for the next 15 years, for a total of $1.5 million. Which offer should Fred accept?
Fred believes he is a savvy investor and can achieve a return of 11% per annum by investing in stocks and bonds. The present value of Giant’s offer for future payments at a discount rate of 11% is $719,086.96. This amount is less than the up-front offer, so Fred takes the lump-sum payment of $750,000.
If Fred accepts the $750,000 and is fortunate enough to realize an 11% return per annum, his investments would realize a future value of $3,588,442 in 15 years.
You can find the future value of annuity with the following calculator:
The Impact of Different Discount Rates
The choice of which discount rate to use when calculating a present value is highly subjective. An investor could decide to use an average inflation rate, for example, because the investor wants to preserve his capital. Or an investor could feel that he could earn a higher return of 11% by investing in the stock market.
Let’s see how different discount rates will affect present values. Take an ordinary annuity that offers annual payments of $30,000 for 20 years. From the formula, the present value of this annuity at a projected inflation rate of 2% will be $490,543. Alternatively, the present value at a discount rate of 11% would be $238,899.84.
Higher discount rates result in lower present values.
Let’s revisit Fred’s offer from Giant Tools. If Fred doesn’t want to spend time studying the stock market and will instead put the money in a savings account paying 3% interest, how does that change Fred’s decision? The present value of 15 annual payments of $100,000 discounted at 3% is $1,193,793.51. In this instance, Fred should accept the payments over 15 years.