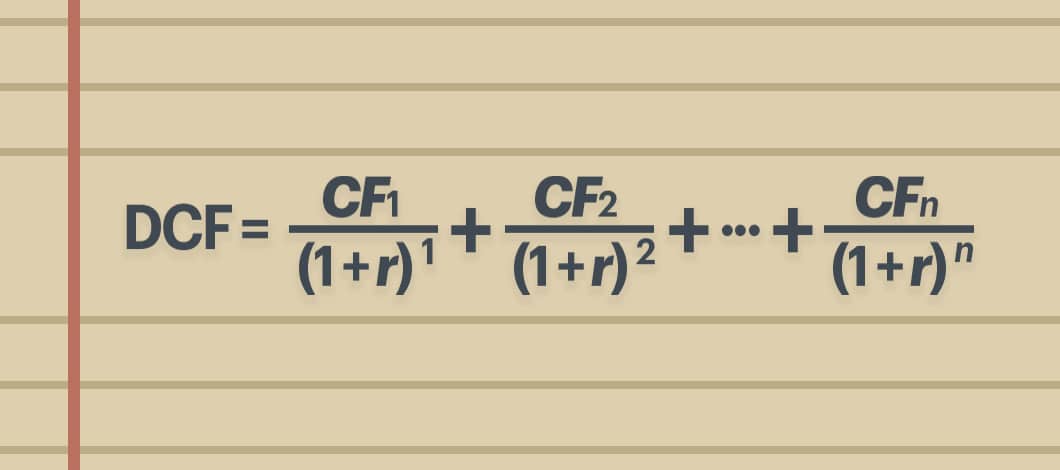As a small business grows, the owner has to constantly make decisions on how and where to invest money. The objective is to invest in those projects that will produce the highest returns.
How does an owner do that? What techniques can an owner use to analyze the different investment alternatives and select the best one? The method that produces the most accurate analysis of the investment alternatives is the discounted cash flow, also known as the net present value (NPV) method.
Let’s look at the pros and cons of the discounted cash flow method and see how it works.
What Are the Methods to Analyze Investment Alternatives?
Analysts and business owners have 3 primary tools to analyze the feasibility of investments or projects.
Payback: The payback method is the length of time it takes for a project to recover the original cost. For example, if the original cost for a project is $400,000, and the project is expected to return $80,000 each year, then the payback period is 5 years. Shorter paybacks are usually better.
The advantage of the payback method is its simplicity, but the disadvantages are that it doesn’t consider the time value of money and doesn’t make any adjustments for risk.
Internal rate of return (IRR): The IRR is the discount rate that results in a net present value of zero for the investment. If a project has an IRR greater than the firm’s weighted average cost of capital, then it should be accepted.
With the IRR method, projects are evaluated relative to the firm’s capital structure, rather than the riskiness of the project or the timing of the cash flows. The IRR method doesn’t indicate the value of a project to the firm.
Discounted cash flow (DCF): The DCF approach calculates the present value of a future stream of cash flows. If the discounted stream of future cash flows is greater than the initial investment, then the project should be accepted. If the net present value is negative, the project should be rejected.
DCF considers the time value of money, allows adjustments to the discount rate to compensate for the riskiness of a project and lets you use different cash flows for each year.
That’s why managers prefer the DCF method. Of all the methods, it weighs the important issues of a project and produces the most accurate results.

How the Discounted Cash Flow Method Works
The discounted cash flow method considers the time value of money. $100 is worth more today than it will be a year from now because of interest costs and inflation rates. If you’re spending money now, you want to know how much you’ll get back and how much it’ll be worth in the future.
That’s what DCF does. It takes projected cash flows and discounts them at an annual rate back to a present value.
DCF has 4 parts:
- Discount rate: The discount rate is a function of the riskiness and uncertainty of the future cash flows, the current interest rates and the company’s weighted average cost of capital. Projects that have higher uncertainties of the outcomes will have higher discount rates. These projects will require a higher rate to justify taking the risk.
- Projected cash flow: These are the cash flows that are projected to come in and out of the project during the time period being analyzed.
- Periods of time: This is the period of time for the expected life of the project. It can be expressed in months, quarters or years.
- Terminal value: The terminal is the future value of the project at the end of the projection period.
What Is the Formula for Discounted Cash Flow?
This is the DCF formula:
Not to worry, though. You don’t have to slog through this math to use the DCF method to evaluate your proposed projects.
There’s a much easier way. You can simply enter your numbers into this free online calculator, and it’ll instantly give you the net present value analysis for the project or investment.
You’ll be able to immediately see if your project has a positive or negative net present value.
Ways to Apply DCF in Your Business
Apply the principal of DCF to your business decision-making process.
These are a few typical applications:
- Valuing a business
- Analyzing the return on a project or investment
- Determining the benefits of a cost-saving proposal
- Buying an expensive piece of equipment
Discounted Cash Flow Example
Suppose you own a restaurant, and you’re considering whether to expand your current facility or to open a completely new store across town. Which alternative would make more sense?
You estimate the cost to expand your current restaurant at $200,000, and your weighted average cost of capital is 8%.
You expect to receive additional cash flow for the first 5 years as follows:
- 1: $50,000
- 2: $55,000
- 3: $57,000
- 4: $60,000
- 5: $60,000
Using the net present value calculator shows the net cash flow as $82,000 and the net present value of the expansion option as $23,635. Because the net present value is positive, the expansion option will be viable.
A New Restaurant
But what about building a new restaurant? Building a new facility is estimated to cost $800,000. Since this is a new operation, it will take some time to build up the clientele in a new market. You estimate the cash flows for the first 5 years for a new store as follows:
- 1: $150,000
- 2: $175,000
- 3: $200,000
- 4: $250,000
- 5: $300,000
Because this is a new market, you’re not as certain about the development and growth of the business. To compensate for this additional risk, you’re going to use a discount rate of 15% instead of 8%.
The calculator shows a net cash flow of $275,000 and a net present value of -$113,645. Because the NPV is negative, opening a new restaurant wouldn’t be acceptable. It would make more financial sense to expand your current facility.
Adjust as Needed
However, what if your projections were too pessimistic? Maybe your restaurant has an excellent reputation, and a new store will attract customers more quickly than you had estimated.
After some thought, you decide to use a discount rate of 12% and revise your cash flow estimates as follows:
- 1: $200,000
- 2: $250,000
- 3: $300,000
- 4: $325,000
- 5: $350,000
Now the calculations show a net cash flow of $625,000 and a net present value of $196,547. Since the net present value is now positive, this analysis shows that opening a new facility is feasible under the revised assumptions.
The purpose of this example is to illustrate the importance of making estimates as accurate as possible. The analysis of opening a new store went from being rejected because of a negative NPV to becoming acceptable with revised projections resulting in a positive NPV.
Since both options are now viable, should you pick one or the other or do both? That decision may hinge on your ability to obtain enough financing for both options. These are the types of decisions business owners have to make, and sometimes it isn’t just about the numbers, it’s about experience and instincts.
Limitations of DCF
While DCF is a great analytical tool, it does have limitations.
Assumptions: The results are only as good as the data that goes into the calculations. Projections of future cash flows and the choice of discount rates are, at best, educated assumptions.
Projections: Forecasting future cash flows can extend for years, possibly even decades. Since the uncertainty of forecasts increases with each year, it’s more practical to limit projection to 5 or 10 years, at the most.
Miscalculations: The calculations of DCL are extremely sensitive. Small differences in the projections or even a small miscalculation can highly skew the results.